以前花をみて感じ考えたことを書いたが、今度は団子をみて感じ考えたことを書く。なぜなら、ある日団子を食べたから。割と有名な団子屋さんなのでご存じの方もいるかもしれないが、そこの団子は3色が串に刺さらずころころ皿に置いてあった。
すると、三つの円に囲まれた部分が気になりだした。そして、それが各円の中心を結んだ三角形に対してどれくらいの割合なのかが気になった。このころはまだ、6角形だと100%敷き詰められるのにな・・くらいに思っていた。
それで、三角形を取り出してみると・・
円の半径を1として・・
スキマの割合はこのようになる。
インターネットで「1-pi/(2*sqrt3)」と入力すると、0.0931・・と計算してくれる。というわけでスキマは約9%なのであるが、インターネットの検索結果のなかにとんでもないものをみつけた。
なんと、「円周率÷(2×ルート3)」は級数展開できるというのだ。しかも、その証明方法もいくつか紹介されていた。フーリエ級数を使ったものが美しかったので、ここでも説明する。
まず、フーリエ級数の有名な式に、「エックス=円周率÷3」を代入する。
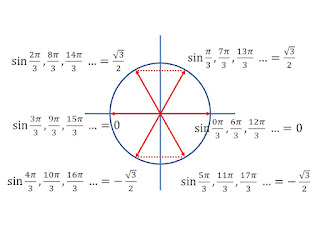
すると、二番目の式にでてくる三角関数の値は下図のようになるので・・
右辺に分数が羅列されているが、これを「1・4・5・8・9・・番目(グループA、赤)」と「2・3・6・7・・番目(グループB、青)」に分ける。
さあ、ここが肝心なのだが、Bを2倍すると、A-Bになっている!
・・と言われても分かりにくいかもしれないから、A+Bと2Bを並べて、足し合わせてみると、Bの部分が消えていく。
そんなわけで、一番下の式から「B=A/3」となる。これを★に代入すると、
結局、スキマの割合は、「1ーA」というわけで、「(5、5+6、5+6+6・・分の1の和)ー(7、7+6、7+6+6・・分の1の和)」になる。
花もいいが、団子もいい。今回は二次元にしたが、三次元にした時に正四面体にしめるスキマ空間の割合なんかも、おそらく円周率などで表現でき、それを級数展開することも可能なのだろう。ちょっとした日常のなかにも、奥深さが垣間見えるものである。