レシート幾何学 101

　以前から素数に関心を持っていたが、本屋さんで『素数姫の素数入門』（「素数に恋する女」製作委員会）という本があるのをみつけ楽しく読んでいる。そのなかにスタニスワフ・ウラムという数学者が、学会でほかの発表が退屈だったため手元のメモ用紙に落書きしていて「ウラムのらせん」をみつけたというエピソードがあった。

　きょうは、それに触発されて書いている。

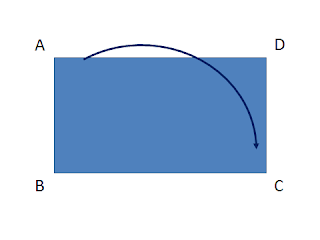
　通勤電車のなかで、胸ポケットに入っていたレシートをいじっていた。下図の長方形をレシートとして、AとCをくっつけるように折る。

　そして開く。

　すると、A・P2・C・P1というひし形ができる。

　これだけでも感動したが、AとCをつけるように折らずにP1、P2の位置を決めることはできないか？という疑問がうまれた。さいしょは長方形の長い辺と短い辺の2変数で表そうとしたが複雑そうなので、短い辺を1、長い辺をx、求めたい長さをyにしてみた。

すると求めたい長さyは、三角形ABP1でピタゴラスの定理をつかえば求められる。

　得られた二次方程式を、解いてみる。

　y = 1/2 ( x - 1/x )。ひし形らしい、対照的で簡潔で美しい式。きっと、何百年、あるいは、何千年も前に発見されているだろう。名前もあるかもしれない。でも独力でたどりついたのはうれしいし、作業に没頭するのは楽しい。学ぶ楽しみを、続けて生きたい（「レシート幾何学」なんて本になるかも；写真はこちらから）。